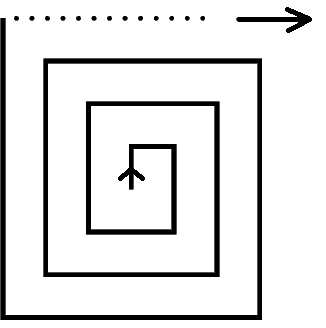
Se desea pintar cada rectángulo de una cuadrícula $5\times5$, usando los colores amarillo, azul, rojo y verde. Con la distribución inicial de colores en la figura dada, ¿cuáles colores podrían estar en la casilla con interrogante, si ningún rectángulo de la cuadrícula puede compartir vértices, ni lados con casillas de igual color?

You want to paint each rectangle of a $5\times5$ grid, using the colors yellow, blue, red and green. With the initial distribution of colors in the given figure, which colors could be in the box with question mark, if no rectangle of the grid can share vertices, or sides with squares of the same color?

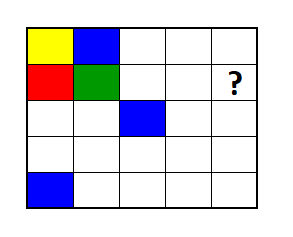
A) Rojo/Red

Observe que la casilla en la fila 3, columna 2, comparte con los colores rojo y azúl un vértice y con el verde un lado. De aquí dado que esta casilla ya comparte con tres colores, la única opción para rellenarla es con amarillo.

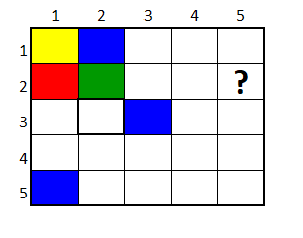
De forma similar, se tiene que la casilla en la fila 2, columna 3, comparte vértices y lados con los colores azúl, verde y amarillo. Por lo tanto, como esta casilla comparte con tres colores, solo se puede rellenar con color rojo.

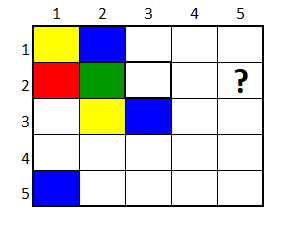
Continuando de forma análoga, la casilla en la fila 1, columna 3, se rellena con amarillo.

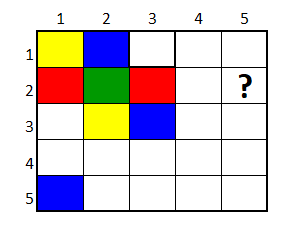
Repitiendo el proceso descrito, se encuentra que la casilla con interrogante se completa con el color rojo.

Note que se debe tener cuidado al concluir la respuesta de inmediato, pues una condición del problema es que a partir de la distribución inicial se debe rellenar totalmente la cuadrícula con los cuatro colores.

Continuamos rellenando la cuadrícula, al pintar de azúl la casilla en la fila 3, columna 1.

Finalmente, manteniendo la idea propuesta se rellena toda la cuadrícula y se confirma que la casilla con interrogante es roja.

Hay cuatro habitaciones numeradas de 1 a 4. En una de ellas está escondido un león. En la puerta de la habitación 1 se lee: "El león está en la habitación 2 o en la 3". En la puerta de la habitación 2 se lee: "El león está en la habitación 3 o en la 4". En la puerta de la habitación 3 se lee: "El león está en la habitación 1 o en la 4". En la puerta de la habitación 4 se lee: "El león no está aquí". Si 3 de esas 4 afirmaciones son verdaderas, ¿detrás de qué puerta está el león?

There are four rooms numbered from 1 to 4. In one of them a lion is hidden. At the door of room 1 it reads: "The lion is in room 2 or in room 3". At the door of room 2 it reads: "The lion is in room 3 or in room 4". At the door of room 3 it reads: "The lion is in room 1 or in room 4". At the door of room 4 it reads: "The lion is not here" If 3 of those 4 statements are true, behind which door is the lion?

A) 3

Está en la puerta 3 pues es la única posibilidad para que haya 3 afirmaciones verdaderas. Si estuviese detrás de la puerta 1, 2 o 4 habría dos verdaderas y dos falsas.

En un torneo de fútbol internacional participan $30$ equipos, de los cuales $5$ son colombianos. ¿De cuántas formas se puede elegir el primer partido, si los colombianos no se pueden enfrentar entre sí?

In an international soccer tournament $30$ teams participate, of which $5$ are Colombian. How many ways can the first match be chosen, if the Colombians can not face each other?

A) 425

El número de formas en que se puede jugar el primer partido está dado por $\binom{25}{2}+25\times 5=\binom{30}{2}-\binom{5}{2}=425$

Los divisores positivos propios de un número $n$, son todos aquellos divisores positivos distintos a él mismo. Sólo hay dos números que satisfacen que la suma de sus divisores propios es 6. ¿Cuál es la diferencia positiva entre estos números?

The proper positive divisors of a number $n$, are all those positive divisors other than $n$ itself. There are only two numbers that satisfy that the sum of their proper divisors is 6. What is the positive difference between these numbers?

A) 19

Como los divisores propios de un número son todos distintos, entonces basta analizar la representación del número 6 como suma de números distintos: $6=1+2+3$, $6=2+4$, $6=1+5$.

Como 1 es divisor de todo número, entonces la representación $6=2+4$ no nos sirve. Ahora bien, tenemos dos números, un primer número, donde sus divisores propios son 1, 2 y 3. Y otro, donde sus divisores propios son 1 y 5. Así entonces, los números cuya suma de sus divisores propios sea 6 son los números 6 y 25. Por lo tanto la diferencia positiva es $25-6=19.$

Considere el siguiente círculo y hexágono regular (con sus seis lados congruentes) tal como se muestra en la figura.

Consider the following circle and regular hexagon (six congruent sides) as it is shown in the picture.

El segmento $AB$ es a su vez un lado del hexágono y un diámetro del círculo. Sean $a$ y $b$ las áreas del círculo y del hexágono, respectivamente. ¿El valor de la expresión $\frac{a}{b}$ es?

The segment $AB$ is a side of the hexagon and the diameter of the circle. Let $a$ and $b$ the areas of the circle and the hexagon respectively. What is the value of $\frac{a}{b}$ ?

A) $\dfrac{\pi}{6 \sqrt{3}}$

Sea $R$ el radio de la círculo, por tanto el lado del hexágono es $2R$. Tenemos que el área del circulo es $b = \pi R^2$. Para calcular el área del hexágono dividamos el hexágono en seis triángulos equiláteros congruentes entre sí.

Por tanto, el área del hexágono es calcular seis veces el área del triángulo equilátero de lado $2R$. Sea $X$ la altura de uno de los seis triángulos por Teorema de Pitagóras obtenemos $4R^2 = R^2 + X^2$, es decir, $X = \sqrt{3}R$.

Por tanto, el área del triángulo equilátero es $\sqrt{3}R^2$ y el area del hexágono $b = 6\sqrt{3}R^2$.

Concluimos que $\frac{a}{b} = \frac{\pi R^2}{6\sqrt{3}R^2} = \frac{\pi }{6\sqrt{3}}$.

Juan contó cuantos cuadrados hay en un cuadrado (tomando en cuenta el orginal) y afirmó: un cuadrado de lado 1 tiene un cuadrado, un cuadrado de lado 2 tiene 5 cuadrados, un cuadrado de lado 3 tiene 14 cuadrados. ¿Un cuadrado como el del tablero de ajedrez, es decir 8x8, cuántos cuadrados tiene?

Juan determined how many squares are in a square (taking in account the original one) and claim: a square of a side of length 1 has a square, a square with a side of length 2 has 5 squares, a square of length 3 has 14 squares. If a square is like a chess board, i.e. $8 \times 8$, how many squares are inside?

A) 204

Un cuadrado de lado 1 tiene un cuadrado.

Un cuadrado de lado 2 tiene un cuadrado de lado 2 y 4 cuadrados de lado 1, para un total de 5 cuadrados, es decir $1^2+2^2=5$.

Un cuadrado de lado 3 tiene un cuadrado de lado 3 y 4 cuadrados de lado 2 y 9 cuadrados de lado 1, para un total de

$1+4+9=1^2+2^2+3^2 =14.$

Un cuadrado de lado 8 tiene

$1^2+2^2+3^2+4^2+5^2+6^2+7^2+8^2 =\1+4+9+16+25+36+49+64 =\204$

cuadrados.

Sean $u$ y $v$ números reales tales que $3^u=4$ y $8^v=9$. ¿Cuál es el valor del producto $uv$?

Let $u$ and $v$ real numbers such that $3^u=4$ and $8^v=9$. What is the value of the product $uv$?

A) $\frac{4}{3}$

$2^{3uv}=8^{uv}=9^u=3^{2u}=(3^u)^2=4^2=16$, de donde $3uv=4$ y $uv=\frac{4}{3}$.

Mónica quiere visitar a su amiga Karen en su nuevo apartamento, para ello sigue las indicaciones de su amiga: Viajar primero al norte 10 metros, girar a la derecha 10 metros y continuar siempre girando a la derecha en la siguiente sucesión $20\;$ metros, $20\;$ metros, $30\;$ metros, $30\;$ metros, ... hasta completar $2400\;$ metros ¿Cuántas veces giró Mónica a la derecha?

Mónica wants to visit her friend Karen at her new apartment, in order to do that, she follows her friend instructions: To travel first north, 10 meters, turn right 10 meters and continue turning right in the following way: $20\;$ meters, $20\;$ meters, $30\;$ meters, $30\;$ meters, ... in this way until you complete $2400$ meters. How many times did Monica turn right?

A) 29

La figura muestra la forma del recorrido de Mónica:

Para saber la cantidad de giros de Mónica debemos resolver la ecuación

\begin{eqnarray*}
10+10+20+20+ \cdots +10n+10n&=&2400 \
10(1+1+2+2+\cdots +n+n)&=&2400\
10 \times 2(1+2+3+\cdots n)&=&2400\
10 \times 2 \times \frac{n(n+1)}{2}&=&2400
\end{eqnarray*}
Esta última ecuación es equivalente a
\begin{eqnarray*}
n(n+1)&=&240\
n^2+n&=&240\
n^2+n-240&=&0
\end{eqnarray*}
Usando la formula cuadrática tenemos que $n=15$ o $n=-16$. Tomamos la solución positiva y así tenemos $n=15$, esto es en total hace $2*15-1=29$ giros a derecha.

Sea $ABC$ un triángulo de área $4$ cm$^2$. Suponga que $\overline{AC}$ se divide en cuatro partes iguales, con segmentos paralelos a $\overline{AB}$. Determine el área en cm$^2$ de la región sombreada, si las líneas punteadas son paralelas a $\overline{BC}$. No escriba las unidades en su respuesta.

Let $ABC$ be a triangle with an area of $4$ cm$^2$. Assume that $\overline{AC}$ is divided in four equal parts, with segments parallel to $\overline{AB}$. Determine the area in cm$^2$ of the shaded region, if the dotted lines are parallel to $\overline{BC}$. Do not write the units in your answer.

1

Al extender las líneas punteadas se tiene la siguiente figura.

Luego al subdividir los paralelogramos en triángulos, se obtiene un total de 16 triángulos y de estos, 4 están sombreados.

Así el área sombreada equivale a

$\dfrac{4}{16}\times4\text{cm}^2=1\text{cm}^2.$

Se tienen dos relojes de agujas, uno verde y uno azul, que inicialmente marcan la hora correcta. El reloj verde se adelanta 10 segundos cada hora, y el reloj azul se retrasa 12 segundos cada hora. ¿Cuántos días deben transcurrir para que los dos relojes marquen la hora correcta nuevamente?

We have two watches with hands, one green and one blue, that initially mark the correct time. The green watch is fast by 10 seconds each hour, and the blue watch is slow by 12 seconds each hour. How many days must pass so that both watches show the correct time simultaneously?

900
900 días
900 dias

Reloj Verde: Por cada dia el reloj verde adelanta $24\times10=240$ segundos, es decir, 4 minutos.
Para que vuelva a marcar la hora correcta, debe adelantar 12 horas, es decir 720 minutos. Eso lo hace en $720 \div 4$= 180 días.
Reloj Azul: Por cada 10 horas el reloj azul retrasa 120 segundos, es decir, 2 minutos.
Debe retrasar 12 horas, es decir, 720 minutos. Eso lo hace en $(720\div 2)\times 10= 3600$ horas, es decir 150 días.
Para que ambos relojes marquen simultáneamente la hora correcta de nuevo, se calcula el m.c.m. de 180 y 150, dando como resultado 900 días.

Colocamos 5 puntos en línea recta de izquierda a derecha. Cada uno de estos puntos es coloreado con uno de 7 colores de tal forma que tres puntos consecutivos no pueden tener el mismo color. ¿Cuántas formas existen de colorear los puntos?

We place 5 points on a line from left to right. Each of these points is colored with one of 7 colors in such a way that three consecutive points cannot have the same color. In how many way can the points be colored?

15876
15,876
15.876

Lo hacemos por complemento. Existen $7^5=16807$ formas de colorear los 5 puntos con 7 colores. Contamos de acuerdo al máximo número de puntos que son coloreados con el mismo color.

Si el máximo es menor que $3$, no tenemos casos que contar.

Si el máximo es igual $3$, entonces tenemos 7 formas de escoger el color que va estar en los tres puntos consecutivos, además, tenemos 3 formas de poner estos tres puntos en la fila de puntos y $6^2=36$ formas de escoger los colores para los puntos restantes. En total son $7\cdot 3\cdot 36=756$.

Si el máximo es igual a 4 puntos del mismo color hay 7 formas de escoger el color que va estar en estos cuatro puntos, hay 4 formas de organizarlos para que queden los tres consecutivos y 6 es el número de colores que podemos escoger para el punto sobrante. En total hay $7\cdot 4\cdot 6=168$.

Si el máximo de puntos del mismo color es 5, son 7 opciones.

En concusión existen 16807-756-168-7=15876 formas de colorear los puntos con la condición pedida.

Usando cada cifra del cero al nueve, hallar los dos números de cinco cifras los mayores posibles tales que su diferencia sea igual a 2019.

¿Cuál es la suma de estos dos números?

Using each digit from zero to nine, find the largest two five-digit numbers such that their difference is equal to 2019.

What is the sum of these two numbers?

140985
140,985
140.985

ABCDE+2019=FGHIJ.

Para que $C \neq H$, $D=8$ ó $D=9$. Consideremos el caso $D=8$.

Si $D=8$ entonces $B=9$ (para que $A \neq F$). Por tanto $G=1$, $I=0$, $F=A+1$, $H=C+1$.

Para hacer la suma los más grande posible hacemos $A=6$, $F=7$, $C=4$, $H=5$, $E=3$, $J=2$.

Luego 71502-69483=2019, de donde 71502+69483=140985.

El análisis del caso $D=9$ es casi idéntico, pero resulta en una suma menor, por lo que se descarta.