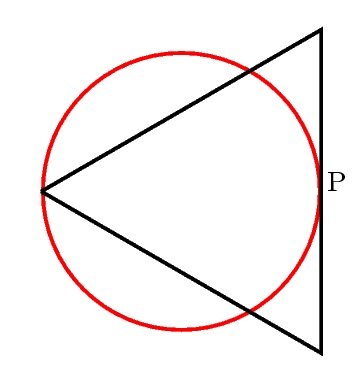
Considere el triángulo equilátero y el círculo mostrados en la figura. Ambos son tangentes en el punto $P$. El cociente del perímetro de la circunferencia sobre el perímetro del triángulo es:

Consider the equilateral triangle and the circle shown in the figure. Both are tangent at the point $P$. The quotient between the circumference and the perimeter of the triangle is:

A) $\frac{\pi}{2\sqrt{3}}$

Llamemos $r$ a la medida del diámetro de la circunferencia y $x$ a la medida de un lado del triángulo equilátero. Tenemos que, el perímetro de la circunferencia en términos de $r$, es $2 \pi \frac{r}{2} = \pi r$ y el del triángulo es $3x$. Dado que el segmento formado desde el punto $P$ hasta el vértice opuesto en el triángulo es un diámetro perpendicular a la recta se sigue por el Teorema de Pitágoras la relación $r^2 + \frac{x^2}{4} = x^2$. Así, $r= \frac{\sqrt{3}x}{2}$ y el cociente pedido es $\frac{\pi}{2\sqrt{3}}$.

¿Cuál es el residuo que deja al dividir entre 5 la siguiente suma?

$4 + 4^2 + 4^3 + 4^4 + · · · + 4^{2018}$

What is the reminder when the following sum is divided by 5?

$4 + 4^2 + 4^3 + 4^4 + · · · + 4^{2018}$

A) 0

Teniendo el cuenta el algoritmo de la division tenemos que:

$4 = 5(0) + 4$
$4^2 = 4(5(0) + 4) = 5(0) + 16 = 5(3) + 1$
$4^3 = 5(3 × 4) + 4$
$4^4 = 5(3 × 4^2) + 4^2 = 5(3 × 4^2 + 3)+ 1$

$4^5 = 5(3 × 4^3 + 3 × 4)+ 4$

Continuado con este procedimiento, se puede observar que todas las potencias de 4 con exponente impar dejan residuo 4 cuando se dividen entre 5; mientras que las potencias impares de 4 dejan residuo 1. De modo que la suma de una potencia impar con una potencia par de 4 deja residuo 0 cuando se divide entre 5. Por lo tanto, dividir $(4 + 4^2) + (4^3 + 4^4) + · · ·+(4^{2017} + 4^{2018})$ entre 5 deja residuo 0.

Alicia miente los días lunes y miércoles, Felicia miente los martes y jueves, Patricia miente los miércoles y viernes y Malicia miente los jueves y sábados. Ellas dicen la verdad los otros cinco días de la semana. Si todas dicen "ayer mentí", ¿cuál día de la semana era ayer?

Alicia lies Mondays and Wednesdays, Felicia lies Tuesdays and Thursdays, Patricia lies Wednesdays and Fridays and Malicia lies Thursdays and Saturdays. They all say the truth the other five days of the week. If they all say "yesterday I lied", which day of the week was yesterday?

A) Miércoles

Alicia puede decir "ayer, mentí" desde el lunes hasta el jueves, porque hoy miente y ayer dijó la verdad, o lo contrario. Felicia puede decirlo desde el martes hasta el viernes, Patricia desde el miércoles hasta el sábado y Malicia desde el jueves hasta el domingo. El único día común es el jueves. Por lo tanto, ayer era miércoles.

Sea $ABCD$ un rectángulo de área $s$. $E$ un punto del segmento $AB$ de modo que $\overline{AE}=\dfrac{1}{3}\overline{AB}$, y $F$ el punto de corte de las prolongaciones de los segmentos $DE$ y $CB$. Hallar el área del triángulo $EBF$ en términos de $s$.

Let $ABCD$ be a rectangle of area $s$. $E$ is a point on the segment $AB$ such that $\overline{AE}=\dfrac{1}{3}\overline{AB}$, and $F$is the intersection of the extensions of segments $DE$ and $CB$. Find the area of triangle $EBF$ in terms of $s$.

A) $\dfrac{2}{3}s$

Como $\overline{AE}=\dfrac{1}{3}\overline{AB}$, entonces $\overline{AB}-\overline{EB}=\dfrac{1}{3}\overline{AB}$. Luego, $\overline{EB}=\dfrac{2}{3}\overline{AB}$. Es inmediato que los triángulos $EBF$ y $DCF$ son semejantes, por lo tanto \begin{align*} \dfrac{\overline{DC}} {\overline{EB}} &=\dfrac{\overline{CF}}{\overline{BF}} .2cm] \dfrac{\overline{AB}}{\frac{2}{3}\overline{AB}} &=\dfrac{\overline{CB}+\overline{BF}}{\overline{BF}}.2cm] \overline{BF} &=2\overline{CB} \end{align*} Finalmente, el área del triángulo $EBF$ es $\dfrac{1}{2}\overline{EB}\cdot\overline{BF}=\dfrac{1}{2}\left(\dfrac{2}{3}\overline{AB}\right)(2\overline{CB})=\dfrac{2}{3}s$

El revés de un número dado es el resultante de escribir sus dígitos en sentido contrario. Por ejemplo, $301$ es el revés de $103$. ¿Cuántos números de 4 dígitos son tales que su revés es de $4$ dígitos y la suma de él y su revés es $9999$?.

The reverse of a given number is the result of writing it with the digits backward. For example, $301$ is the reverse of $103$. How many 4-digit numbers are there such that its reverse is a 4-digit number and the sum of it with its reverse is $9999$?

A) 80

Notemos que el primer dígito y el último deben sumar $9$. Si juntamos estos dos dígitos los números que cumplen con la propiedad que sus dos dígitos sumen $9$ son $18,27,36,45,54,63,72,81.$
Dado que el segundo y tercer dígito también deben sumar $9$, para encontrar todos los números con esta propiedad basta tomar cada uno de éstos e intercalar entre el primer y último dígito todos los demás incluyendo el mismo, así con el 18 tenemos $1\underline{18}8$,$1\underline{27}8$,$1\underline{36}8$, etc

Así por cada numero de dos dígitos tenemos 8 números por tanto podemos obtener así $8 \times 8=64$ números con esta propiedad.

Notemos que los dígitos $0$ y $9$ no pueden aparecer en la primera y cuarta posición sin embargo pueden aparecer en la segunda y tercera, así en medio de cada uno de los números de dos dígitos del conjunto de arriba escribimos los dígitos $09$ y $90$, así por ejemplo obtenemos $1\underline{09}8$,$1\underline{90}8$,$2\underline{09}7$,$2\underline{90}7$, etc. De esta manera por cada numero del conjunto $18,27,36,45,54,63,72,81$
obtenemos $2$ números con la propiedad, así tenemos $16$ números más. Por lo anterior en total tenemos $64+16=80$ números.

Considere $ABCDE$ un pentágono regular de lado 1. Las diagonales $AD$ y $EB$ se cortan en un punto $P$. Calcular el perímetro del cuadrilátero $PBCD$

Consider the regular pentagon $ABCDE$ with side 1. Diagonals $AD$ and $EB$ meet at the point $P$. Find the perimeter of the quadrilateral $PBCD$

A) 4

El angulo interior de un pentágono regular mide 108.
El triangulo EAB es isosceles, con AE = AB y ∠EAB = 108, de donde
∠AEB = ∠ABE = 36.
Luego ∠EBC = 72 y asi ∠EBC + ∠BCD = 180. Se sigue que EB||DC.
De manera análoga se obtiene que AD||BC.
Por lo tanto el cuadrilátero PBCD es un paralelogramo, que además tiene dos
lados consecutivos iguales, por lo que es un rombo.
En conclusión el diámetro de PBCD es igual a 4.

Una circunferencia divide al plano en dos regiones. Dos circunferencias secantes lo dividen en 4 regiones. ¿En a lo más cuántas regiones queda dividido el plano por 100 circunferencias secantes dos a dos?

Nota: Dos circunferencias son secantes si tienen exactamente dos puntos en común.

A circle divides the plane in two regions. Two secant circles divide the plane in 4 regions. In at most how many regions is the plane divided by 100 circles such that any two circles are secant?

Note: Two circles are secant if they have two common points.

A) 9902

Para obtener el máximo número de regiones, consideremos la configuración en la que tres circunferencias no pasan por el mismo punto. Si ya se han trazado $n$ circunferencias, la siguiente corta a las anteriores en $2n$ puntos y ella misma queda dividida en $2n$ arcos. Cada uno de esos arcos divide a una de las regiones anteriores en dos partes, por lo tanto el número de regiones aumenta en $2n$. Como una circunferencia divide al plano en dos regiones, agregando otras 99 se obtienen
$2 + 2(1+2+3+\cdots+99) = 2+100\cdot 99=9902$
regiones.

¿Cuántas tripletas ordenadas $(a,b,c)$ de números enteros positivos impares satisfacen que $a+b+c=41$?

How many ordered triplets $(a,b,c)$ of odd positive integers satisfy that $a+b+c=41$?

A) 210

Podemos escribir $a=2p+1,$ $b=2q+1,$ $c=2r+1$ donde $p,q,r$ son números enteros positivos.

Así la ecuación nos queda $2p+2q+2r=38$ y al simplificar obtenemos $p+q+r=19$.

Para obtener el resultado debemos hacer una combinación con repetición donde tenemos 19 objetos para escoger de tres tipos, $p,q,r$, es decir, $\binom{19+3-1}{3-1}=\binom{21}{2}=210$.

Sean $p$ y $q$ dos números primos diferentes tales que $p+q$ y $p-q$ también son primos. ¿Cuál es el valor del producto $pq$?

Let $p$ and $q$ be two different prime numbers such that $p+q$ and $p-q$ are also prime numbers. What is the value of the product $pq$?

10

Si $p$ y $q$ fuesen ambos pares o ambos impares entonces $p+q$ sería par y mayor que 2, y no sería primo. Luego uno es par y otro impar. El par sólo puede ser $q$, luego $q=2$ y $p-2$, $p$ y $p+2$ son primos. Pero estos tres números dejan restos diferentes en la división entre 3, luego uno de ellos debe ser múltiplo de 3, y como es primo debe ser 3. la única posibilidad es que sea $p-2=3$ (de lo contrario sería $p-2\le 1$). Luego $p=5$ y $pq=10$.

Cada segundo, un niño da un paso a la derecha, o da un paso a la izquierda, o se queda quieto. Después de tres segundos, ¿cuántas, de todas los posibles acciones del niño, lo dejan de vuelta en su posición inicial?

Each second, a boy either takes a step to the right, or one to the left, or stays put. After three seconds, how many of all actions of the boy leave him in the original position he started out in?

7

Hay dos formas de quedar en la posición inicial: (a) cada segundo el niño se queda quieto, (b) un segundo quieto, otro a la derecha y otro a la izquierda. La segunda opción puede ocurrir de 6 formas distintas. Así que la respuesta es 7.

Un capicúa es un número que se lee igual de derecha a izquierda como de izquierda a derecha; por ejemplo, 544989445 es un capicúa. Si la suma de dos capicúas de cuatro dígitos es un capicúa de cinco dígitos, hay sólo dos sumas posibles. ¿Cuál es la diferencia positiva entre ellas?

A capicua is a number that reads the same forward and backward; for example 544989445 is capicua. If the sum of two four-digit capicua is a five-digit capicua, there are only two possible sums. What is the positive difference between them?

1210
1,210
1.210

$abba+cddc=xyzyx$ tiene que ser $x=1$, luego $a+c=11$, por lo tanto $y=1$ ó $2$.

Si $y=1$, entonces $b+d=0$ y la suma es $11011$.

Si $y=2$, entonces $b+d=11$ y la suma es $12221$.

$12221-11011=1210$.

Si $a$, $b$ y $c$ son números enteros positivos tales que $(a+b)(a+c)=91$ y $(a+b)(b+c)=156$. Hallar el valor de $abc$.

If $a$, $b$ and $c$ are positive integer numbers such that $(a+b)(a+c)=91$ and $(a+b)(b+c)=156$. Find the value of $abc$.

108

Los números 91 y 156 tienen un divisor común y este es 13, así $a+b=13$ ya que esta en las dos ecuaciones. Al dividir, obtenemos que $a+c=7$ y $b+c=12$.

Aquí tenemos un sistema de ecuaciones $3\times 3$, en el cual al sumar las tres ecuaciones obtenemos que $2(a+b+c)=32$ lo que implica que $a+b+c=16$ de donde obtenemos que $a=4$, $b=9$ y $c=3$ y por lo tanto que $abc=108$