Si $128^2+4^7=2^n$, halle el valor de $n$.

If $128^2+4^7=2^n$, find the value of $n$.

A) 15

$2^n=(2^7)^2+(2^2)^7=2\cdot 2^{14}$. Por tanto $n=15$.

En una reunión donde se encuentran personas racionales, que siempre dicen la verdad, y personas imprecisas, que siempre mienten, se encuentran tres matemáticos famosos: Gauss, Euler y Noether. Cada uno hace una afirmación:

Gauss dice: “Noether es imprecisa”.
Euler dice: “Gauss y Noether pertenecen a grupos distintos”.
Noether dice: “Yo soy racional”.

¿Cuál de las siguientes es correcta?

In a meeting where there are rational people, who always say the truth, and imprecise people, who always lie, there are three famous mathematicians: Gauss, Euler, and Noether. Each one makes a statement:

Gauss says: “Noether is imprecise”.
Euler says: “Gauss and Noether belong to different groups”.
Noether says: “I am rational”.

Which of the following is correct?

A) Euler es racional, Noether es imprecisa y Gauss es racional.

Si Noether miente entonces Gauss tiene la razón, entonces Gauss es racional, Noether es imprecisa y Euler racional.

Si Noether dice la verdad, Gauss miente y Euler dice la verdad y es racional.

Si Euler dice la verdad, Gauss es racional, Noether es imprecisa y por tanto Euler racional.

Halle la suma de todos los números impares positivos de dos cifras que son múltiplos del producto de sus cifras.

Find the sum of all odd, positive, two-digit numbers which are multiples of the product of their digits.

A) 26

Sea $\overline{ab}$ el número de dos cifras, o sea $\overline{ab}=10\cdot a+b$. Como el número es impar, entonces $b$ debe ser un dígito impar; luego debemos encontrar los dígitos $a,b$ tales que
$10\cdot a+b=k\cdot a\cdot b \quad \text{para algún}\, k\in\mathbb{N},$
es decir,
\begin{equation}
a(k\cdot b-10)=b;\qquad\qquad\qquad\text{(e1)}
\end{equation}
luego $a$ debe ser un divisor de $b$.

Ahora con $a=b$, de (e1) tendríamos $b\cdot k-10=1$, esto es $b\cdot k=11$, luego $b=1$ y $k=11$. Así, el número $\overline{ab}$ es $11$.

Si $a=1$, de (e1) tendríamos $k\cdot b-10=b$, luego $b(k-1)=10$, las posibilidades de $b$ son $1$ y $5$. Con $b=5$ se tiene que $k=3$; por tanto, el número $\overline{ab}$ es $15$.

Ahora como $b$ es impar, o sea $b\in\{1,\,3,\,5,\,7,\,9\}$ y $a$ es divisor de $b$, las posibilidades que quedan son $b=9$ y $a=3$, las cuales no satisfacen la ecuación (e1). En efecto, $3(9k-10)=9\, \Leftrightarrow \, 9k-10=3\, \Leftrightarrow \, 9k=13.$

No existe $k$ natural que satisfaga $9k=13.$ Por lo tanto, los números son $11$ y $15$ y su suma es $26$.

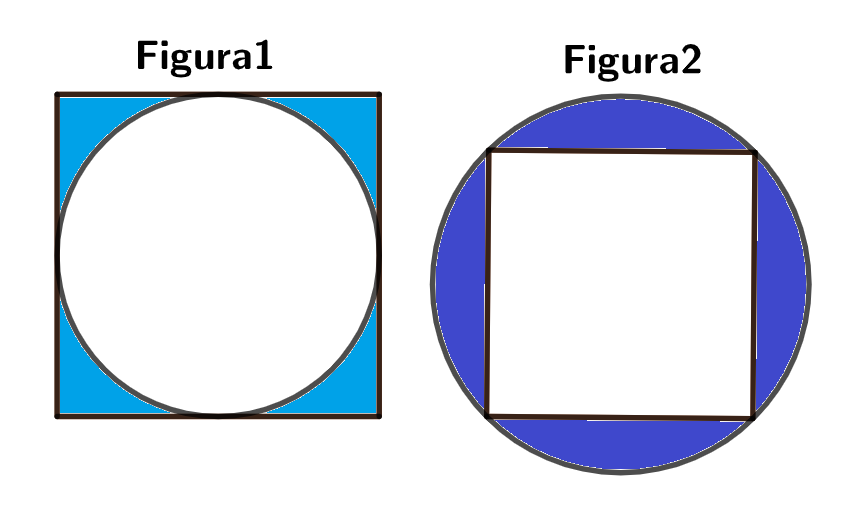
En la figura 1, se tiene un círculo inscrito en un cuadrado; en la figura 2, se tiene un cuadrado inscrito en otro círculo. Si el radio del círculo de la figura 1 es el doble del radio del círculo de la figura 2, encuentre la razón entre el área sombreada de la figura 1 y el área sombreada de la figura 2.

In figure 1, a circle inscribed inside a square is shown; in figure 2, a square inscribed inside another circle is shown. If the radius of the circle in figure 1 is twice the radius of the circule in figure 2, find the ratio of the shaded region in figure 1 and the area of the shaded region in figure 2.

A) $\dfrac{4(4-\pi)}{\pi-2}$

Sean $r$ el radio del círculo inscrito, $A$ el área sombreada de la figura 1 y $R$ el radio del círculo circunscrito, $B$ el área sombreada de la figura 2.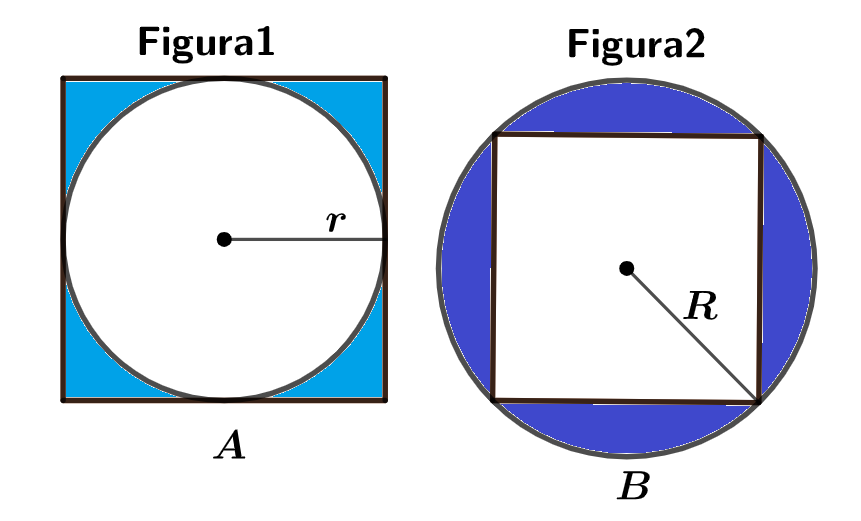

Entonces
$A=(2r)^2-\pi r^2=(4-\pi)r^2\quad \text{y}\quad B=\pi R^2-2R^2=(\pi-2)R^2.$
La razón entre $A$ y $B$ es $\frac{A}{B}=\frac{(4-\pi)r^2}{(\pi-2)R^2}.$
Como $r=2R$, entonces $\frac{A}{B}=\frac{(4-\pi)(2R)^2}{(\pi-2)R^2}=\frac{(4-\pi)4R^2}{(\pi-2)R^2}=\frac{4(4-\pi)}{\pi-2}.$

El reverso de un número consiste en el número que se escribe invirtiendo el orden de los dígitos del número original. Por ejemplo, el reverso de $527$ es $725$ y el reverso de $1086$ es $6801$. Se dice que un número supera a otro si es más grande y su reverso es más grande que el reverso del otro número. Por ejemplo, $527$ supera a $341$ porque $527>341$ y $725>143$; el número $5102$ no supera a $4257$ porque $2015$ no es mayor que $7524$.

¿Cuántos números de cuatro dígitos que empiezan con el dígito $2$ y terminan en el dígito $5$, superan al número $2025$?

The reverse of a number is the number written by reversing the order of the digits in the original number. For example, the reverse of $527$ is $725$, and the reverse of $1086$ is $6801$. A number is said to be grander than another number if it is larger and its reverse is larger than the reverse of the other number. For example, $527$ is grander than $341$ because $527>341$ and $725>143$; the number $5102$ is not grander than $4257$ because $2015$ is not larger than $7524$.

How many four-digit numbers that start with the digit $2$ and end with the digit $5$ ​​are grander than the number $2025$?

A) 79

Para que un número de cuatro dígitos que inicia con el dígito 2 y termina con el dígito 5 sea mayor a 2025, entonces es necesario que el dígito de las centenas sea mayor o igual a 0. De otro lado, para que su reverso sea mayor que el reverso de 2025, esto es, 5202, se requiere que el dígito de las decenas sea mayor o igual a 2.

En otras palabras, para que un número de la forma $2ab5$ (siendo $a$ y $b$ dígitos) supere a 2025, se requiere que $a\geq0$ y $b\geq2$.

Vamos a determinar la solución del problema analizando cuatro posibilidades:

El dígito de las centenas es mayor a 0 y el dígito de las decenas es mayor a 2. Es decir, $a>0$ y $b>2$.
El dígito de las centenas es 0 y el dígito de las decenas es mayor a 2. Es decir, $a=0$ y $b>2$.
El dígito de las centenas es mayor a 0 y el dígito de las decenas es 2. Es decir, $a>0$ y $b=2$.
El dígito de las centenas es 0 y el dígito de las decenas es 2. Es decir, $a=0$ y $b=2$.

En el caso (1) tenemos 9 opciones para el dígito de las centenas (de 1 a 9) y 7 opciones para el dígito de las decenas (de 3 a 9). Luego en total tenemos $9\times7=63$ números posibles, todos ellos superando a 2025.

En el caso (2) tenemos 7 opciones para el dígito de las decenas (de 3 a 9). Luego en total tenemos 7 números posibles (2035, 2045, ..., 2095), todos ellos superando a 2025.

En el caso (3) tenemos 9 opciones para el dígito de las centenas (de 1 a 9). Luego en total tenemos 9 números posibles (2125, 2225, ..., 2925), todos ellos superando a 2025.

En el caso (4) analizamos el número 2025, pero este número no es mayor que 2025; luego este número no supera a 2025.

En conclusión hay 63+7+9=79 números de cuatro dígitos que empiezan con el dígito 2 y que terminan con el dígito 5 que superan al número 2025.

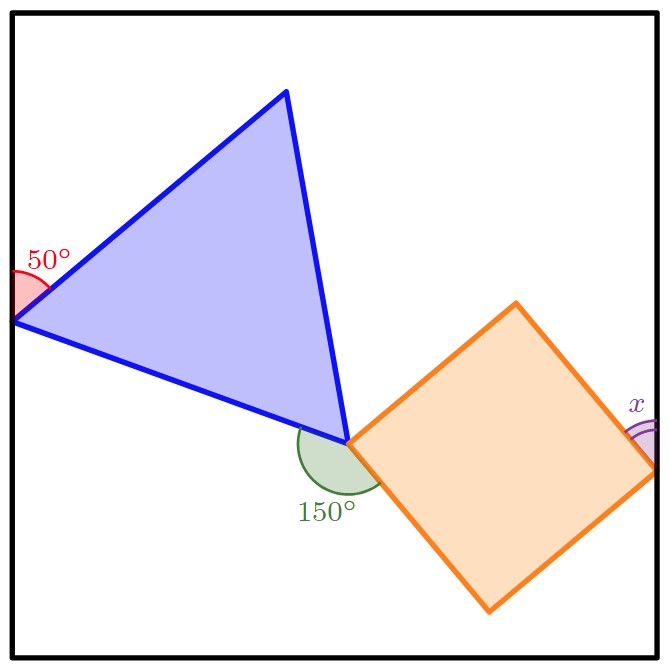
En la siguiente figura se encuentran un triángulo equilátero de color azul y un cuadrado de color naranja dentro de un cuadrado de color negro. El ángulo de color rojo mide $50^\circ$ y el ángulo de color verde mide $150^\circ$. ¿Cuál es la medida en grados del ángulo morado marcado con la letra $x$?

In the following figure, there is a blue equilateral triangle and an orange square inside a black square. The red angle measures $50^\circ$ and the green angle measures $150^\circ$. What is the degree measure of the purple angle marked with the letter $x$?

A) 40

Vamos a considerar el polígono sombreado de azul claro que se muestra en la siguiente figura. Este polígono tiene 7 lados, por tanto, la suma de los ángulos internos de este polígono es $180^\circ\times(7-2)=900^\circ$.

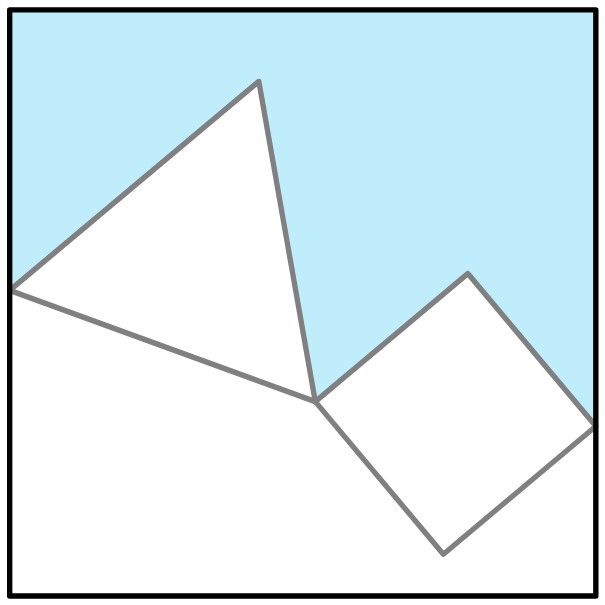
Otra forma de argumentar este hecho se observa en la siguiente figura, donde el polígono se ha subdividido en 5 triángulos internos cuyos vértices son vértices del polígono original. Dado que la suma de los ángulos internos de cada triángulo es $180^\circ$, entonces la suma de los ángulos internos del polígono es $180^\circ\times5=900^\circ$.

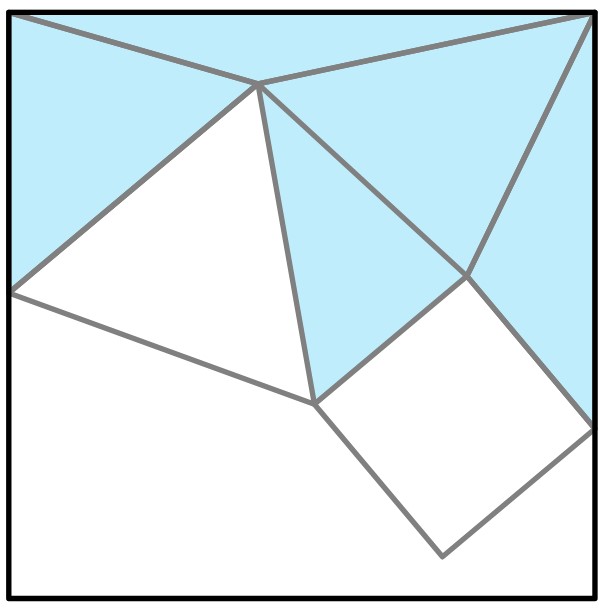
Algunos ángulos internos de este polígono pueden determinarse de la siguiente manera:

En los vértices que son vértices del cuadrado grande se tienen ángulos rectos, esto es, ángulos cuya medida es $90^\circ$.
En el vértice que es vértice del triángulo equilátero, se tienen ángulos suplementarios. Dado que los ángulos internos de un triángulo equilátero miden $60^\circ$, entonces, el ángulo interno del polígono (en este vértice) mide $300^\circ$.
En el vértice que es vértice del cuadrado pequeño, se tienen ángulos suplementarios. Dado que los ángulos internos de un cuadrado miden $90^\circ$, entonces el ángulo interno del polígono (en este vértice) mide $270^\circ$.
En el vértice que es vértice simultáneamente del triángulo equilátero y el cuadrado pequeño, se unen cuatro ángulos cuya suma es $360^\circ$; tres de ellos miden: $150^\circ$ (según la información del problema), $60^\circ$ (ángulo interno del triángulo equilátero) y $90^\circ$ (ángulo interno del cuadrado). Entonces, el ángulo interno del polígono (en este vértice) mide $60^\circ$.

En la siguiente figura se presenta esta información.

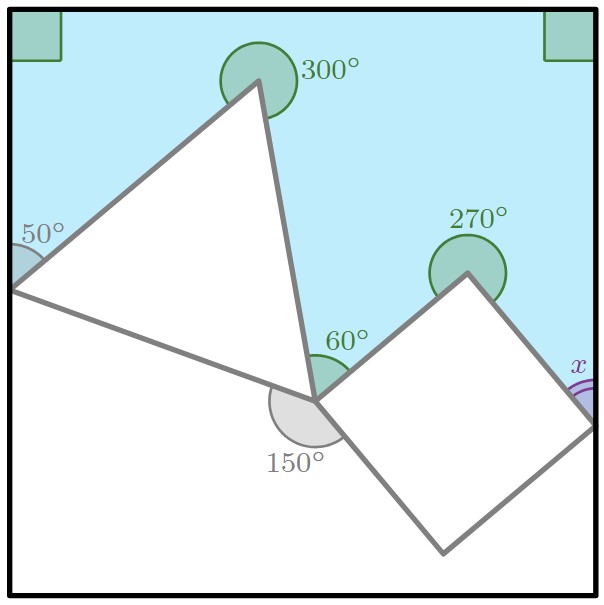
En conclusión, la suma de los ángulos internos del polígono es $50^\circ+90^\circ+90^\circ+x+270^\circ+60^\circ+300^\circ=860^\circ+x,$
la cual debe ser $900^\circ$. Por tanto el ángulo marcado con la letra $x$ debe medir $40^\circ$.

¿Cuántos enteros positivos de dos cifras hay que, al elevarse al cuadrado y después ser divididos entre cinco, dejan un residuo de cuatro?

How many positive two-digit integers are there that, when squared and then divided by five, leave a remainder of four?

A) 36

Sea $n$ un número de dos cifras que cumple la condición. Esto significa que existe un entero $q$ tal que:
$n^2 = 5q + 4.$

Reescribiendo la ecuación:

$n^2 - 4 = 5q.$

Factorizando el lado izquierdo:

$(n - 2)(n + 2) = 5q.$

Dado que $(n - 2)(n + 2)$ es múltiplo de 5, uno de los factores debe ser múltiplo de 5. Es decir, existe un entero $k$ tal que:

$n - 2 = 5k \quad \text{o} \quad n + 2 = 5k$

Despejando $n$:

$n = 5k + 2 \quad \text{o} \quad n = 5k - 2$

Ahora, contamos cuántos valores de $n$ en el rango de dos cifras $(10 \leq n \leq 99)$ cumplen estas formas:

Para $n = 5k + 2$, el mínimo valor en el rango ocurre cuando $k = 2$ ($n = 12$) y el máximo cuando $k = 19$ ($n = 97$). Esto da $18$ valores.
Para $n = 5k - 2$, el mínimo valor en el rango ocurre cuando $k = 3$ ($n = 13$) y el máximo cuando $k = 20$ ($n = 98$). Esto da $18$ valores.

En total, hay $36$ números que cumplen la condición.

Sea $ABCD$ es un cuadrado. Se prolonga $AB$ hasta $M$ de manera que las áreas de $ABCD$ y $DBM$ sean iguales. Encuentre la razón entre $BC$ y la distancia desde $C$ hasta la intersección entre $BC$ y $DM$.

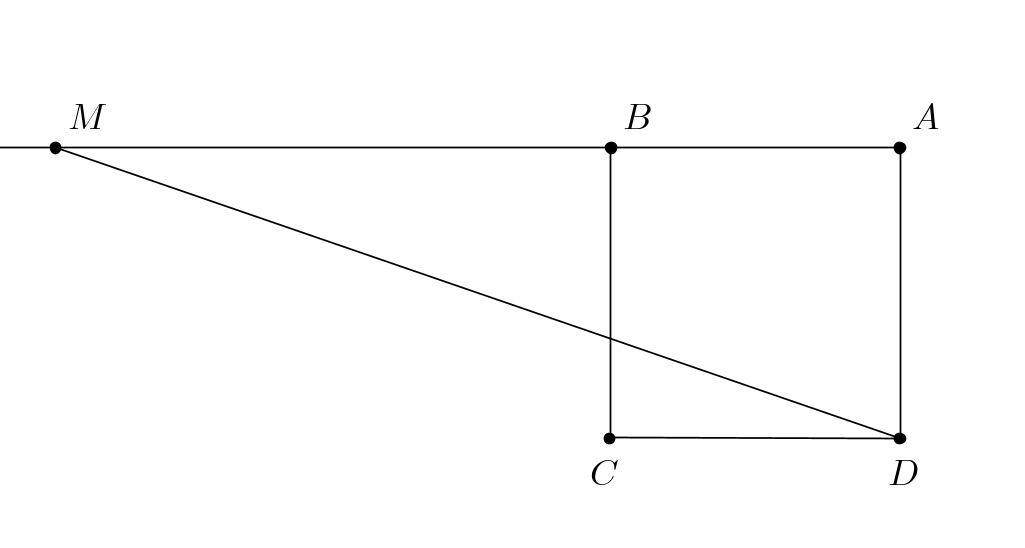
Let $ABCD$ be a square. Extend $AB$ to $M$ such that the areas of $ABCD$ and $DBM$ are equal. Find the ratio of $BC$ to the distance from $C$ to the intersection of $BC$ and $DM$.

A) $3$

Sea $BM = x$, entonces $AM = AB + BM = a + x$. El área del $\triangle DBM=\frac{a(a+x)}{2}-\frac{a^2}{2}$ que lleva a $\frac{a(a+x)}{2}-\frac{a^2}{2} =a^2$ es decir $x=2a$. Nuevamente comparando áreas y llamando con $U$ a la intersección entre $\overline{BC}$ y $\overline{DM}$, $\frac{2a(a-u)}{2} =a^2-\left(\frac{a^2}{2}-\frac{au}{2}\right),$ para obtener $a=3 DU$.

La suma de los dígitos de un número de dos cifras es 7. Si el dígito de las decenas sobrepasa en 3 al dígito de las unidades, hallar el número.

Escriba su respuesta usando sólo números.

The sum of the digits of a two-digit number is 7. If the tens digit is 3 more than the unit digit, find the number.

Write your answer using only numbers.

52

Llamemos $x$ el al dígito de las unidades, entonces

$x+3$ es el dígito de las decenas y

$x+(x+3)=7$ la condición del problema. Al resolver la ecuación

$x+x+3=7$

$2x=7-3$

$2x=4$

$x=2$

Luego, si sobrepasa en tres, el número será 52.

Otra forma es mirar los números de dos dígitos del 10 al 99 y observar cuál de ellos al sumar sus dígitos el resultado es 7 de esta lista, mira la condición de que el digito de las decenas sea mayor en tres unidades.

Una prueba de Olimpiadas de Matemáticas consta de 8 preguntas en total: 5 preguntas de opción múltiple con respuesta única (4 opciones) y 3 preguntas de falso o verdadero. ¿Cuántos estudiantes deben participar como mínimo, para garantizar que dos de ellos tengan las mismas respuestas?

Escriba su respuesta usando sólo números.

A Math Olympiad test consists of 8 questions in total: 5 multiple choice questions with unique answer (4 options) and 3 true or false questions. How many students must participate, at the least, to ensure that two of them have the same answers?

Write your answer using only numbers.

8193
8,193
8.193

Se tienen $4^5= 1024$ formas posibles de responder las preguntas de opción múltiple con única respuesta, por $2^3=8$ formas de responder las de falso o verdadero. Es decir, 8192 formas posibles de responder. Por el principio del palomar, cuando sumamos un participante más, se garantizará que al menos dos de ellos tengan las mismas respuestas.

En la figura dada, $D$ es un punto en el lado $BC$ y $E$ es un punto en el lado $AC$ del triángulo $ABC$, tal que $AD = AE$, $AC = AB$, el ángulo $DAB = 40°$ y el ángulo $ADE = 71°$. ¿Cuánto mide, en grados, el ángulo $ADB$?

Escriba su respuesta usando sólo el número de la medida, sin usar caracteres especiales.

In the given figure, $D$ is a point on the side $BC$ and $E$ is a point on the side $AC$ of triangle $ABC$, such that $AD = AE$, $AC = AB$, the angle $DAB = 40°$ and the angle $ADE = 71°$. What is the measure, in degrees, of angle $ADB$?

Write your answer using only the number of the measure, without using special characters.

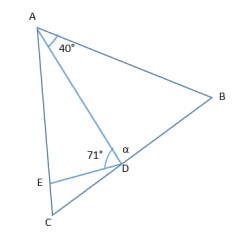
89

Como $AD = AE$, el ángulo $AED$ es igual al ángulo $ADE = 71°$, entonces el $EAD = 180° - 2(71) = 38°$. Luego, el ángulo $CAB = 40° + 38° = 78°$.

Y, como $AC = AB$, el ángulo $ACB = ABC = (180° - 78°) / 2 = 51°$.

Así, finalmente tenemos que el ángulo $ADB = 180° - DAB - ABC = 180° - 40 - 51° = 89°$.

Hallar el valor exacto de

donde los puntos suspensivos indican que la operación se repite infinitamente.

Escriba su respuesta usando sólo números.

Find the exact value of

where the dots indicate that the operation repeats infinitely.

Write your answer using only numbers.

2025
2,025
2.025

Sea

Notando que ese valor de $x$ se repite nuevamente en el paso infinito de la fracción continua, es posible afirmar que

Así, se tendría una ecuación en una incógnita asociada a la expresión, con la que podemos operar de la siguiente manera:

Así,

También es posible partir de la ecuación $x^2+2x=2024$, usar la resolvente cuadrática y hallar los valores $x=44$ y $x=-46$. Pero al ser $x$ una expresión fraccionaria positiva, se descarta el $-46$. Luego,